Площадь треугольника - формулы и примеры решения задач

Ниже приведены формулы нахождения площади произвольного треугольника которые подойдут для нахождения площади любого треугольника, независимо от его свойств, углов или размеров. Формулы представлены в виде картинки, здесь же приведены пояснения по применению или обоснованию их правильности. Также на отдельном рисунке указаны соответствия буквенных обозначений в формулах и графических обозначений на чертеже.

Примечание . Если же треугольник обладает особыми свойствами (равнобедренный, прямоугольный, равносторонний), можно использовать формулы, приведенные ниже, а также дополнительно специальные, верные только для треугольников с данными свойствами, формулы:

• "Формулы площади равностороннего треугольника"

Формулы площади треугольника

Пояснения к формулам :
a, b, c - длины сторон треугольника, площадь которого мы хотим найти
r - радиус вписанной в треугольник окружности
R - радиус описанной вокруг треугольника окружности
h - высота треугольника, опущенная на сторону
p - полупериметр треугольника, 1/2 суммы его сторон (периметра)
α - угол, противолежащий стороне a треугольника
β - угол, противолежащий стороне b треугольника
γ - угол, противолежащий стороне c треугольника
h a , h b , h c - высота треугольника, опущенная на сторону a , b , c

Обратите внимание, что приведенные обозначения соответствуют рисунку, который находится выше, чтобы при решении реальной задачи по геометрии Вам визуально было легче подставить в нужные места формулы правильные значения.

• Площадь треугольника равна половине произведения высоты треугольника на длину стороны на которую эта высота опущена (Формула 1). Правильность этой формулы можно понять логически. Высота, опущенная на основание, разобьет произвольный треугольник на два прямоугольных. Если достроить каждый из них до прямоугольника с размерами b и h, то, очевидно, площадь данных треугольников будет равна ровно половине площади прямоугольника (Sпр = bh)
• Площадь треугольника равна половине произведения двух его сторон на синус угла между ними (Формула 2) (см. пример решения задачи с использованием этой формулы ниже). Несмотря на то, что она кажется непохожей на предыдущую, она легко может быть в нее преобразована. Если из угла B опустить высоту на сторону b, окажется, что произведение стороны a на синус угла γ по свойствам синуса в прямоугольном треугольнике равно проведенной нами высоте треугольника, что и даст нам предыдущую формулу
• Площадь произвольного треугольника может быть найдена через произведение половины радиуса вписанной в него окружности на сумму длин всех его сторон (Формула 3), проще говоря, нужно полупериметр треугольника умножить на радиус вписанной окружности (так легче запомнить)
• Площадь произвольного треугольника можно найти, разделив произведение всех его сторон на 4 радиуса описанной вокруг него окружности (Формула 4)
• Формула 5 представляет собой нахождение площади треугольника через длины его сторон и его полупериметр (половину суммы всех его сторон)
• Формула Герона (6) - это представление той же самой формулы без использования понятия полупериметра, только через длины сторон
• Площадь произвольного треугольника равна произведению квадрата стороны треугольника на синусы прилежащих к этой стороне углов деленного на двойной синус противолежащего этой стороне угла (Формула 7)
• Площадь произвольного треугольника можно найти как произведение двух квадратов описанной вокруг него окружности на синусы каждого из его углов. (Формула 8)
• Если известна длина одной стороны и величины двух прилежащих к ней углов, то площадь треугольника может быть найдена как квадрат этой стороны, деленный на двойную сумму котангенсов этих углов (Формула 9)
• Если известна только длина каждой из высот треугольника (Формула 10), то площадь такого треугольника обратно пропорциональна длинам этих высот, как по Формуле Герона
• Формула 11 позволяет вычислить площадь треугольника по координатам его вершин , которые заданы в виде значений (x;y) для каждой из вершин. Обратите внимание, что получившееся значение необходимо взять по модулю, так как координаты отдельных (или даже всех) вершин могут находиться в области отрицательных значений

Примечание . Далее приведены примеры решения задач по геометрии на нахождение площади треугольника. Если Вам необходимо решить задачу по геометрии, похожей на которую здесь нет - пишите об этом в форуме. В решениях вместо символа "квадратный корень" может применяться функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение . Иногда для простых подкоренных выражений может использоваться символ √

Задача. Найти площадь по двум сторонам и углу между ними

Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника .

Решение .

Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ

Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60

В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов . Он будет равен корню из трех на два.
S = 15 √3 / 2

Ответ : 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)

Задача. Найти площадь равностороннего треугольника

Найти площадь равностороннего треугольника со стороной 3см.

Решение .

Площадь треугольника можно найти по формуле Герона:

S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))

Поскольку a = b = c формула площади равностороннего треугольника примет вид:

S = √3 / 4 * a 2

S = √3 / 4 * 3 2

Ответ : 9 √3 / 4.

Задача. Изменение площади при изменении длины сторон

Во сколько раз увеличится площадь треугольника, если стороны увеличить в 4 раза?

Решение .

Поскольку размеры сторон треугольника нам неизвестны, то для решения задачи будем считать, что длины сторон соответственно равны произвольным числам a, b, c. Тогда для того, чтобы ответить на вопрос задачи, найдем площадь данного треугольника, а потом найдем площадь треугольника, стороны которого в четыре раза больше. Соотношение площадей этих треугольников и даст нам ответ на задачу.

Далее приведем текстовое пояснение решения задачи по шагам. Однако, в самом конце, это же самое решение приведено в более удобном для восприятия графическом виде. Желающие могут сразу опуститься вниз решения.

Для решения используем формулу Герона (см. выше в теоретической части урока). Выглядит она следующим образом:

S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(см. первую строку рисунка внизу)

Длины сторон произвольного треугольника заданы переменными a, b, c.
Если стороны увеличить в 4 раза, то площадь нового треугольника с составит:

S 2 = 1/4 sqrt((4a + 4b + 4c)(4b + 4c - 4a)(4a + 4c - 4b)(4a + 4b -4c))
(см. вторую строку на рисунке внизу)

Как видно, 4 - общий множитель, который можно вынести за скобки из всех четырех выражений по общим правилам математики.
Тогда

S 2 = 1/4 sqrt(4 * 4 * 4 * 4 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - на третьей строке рисунка
S 2 = 1/4 sqrt(256 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - четвертая строка

Из числа 256 прекрасно извлекается квадратный корень, поэтому вынесем его из-под корня
S 2 = 16 * 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
S 2 = 4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(см. пятую строку рисунка внизу)

Чтобы ответить на вопрос, заданный в задаче, нам достаточно разделить площадь получившегося треугольника, на площадь первоначального.
Определим соотношения площадей, разделив выражения друг на друга и сократив получившуюся дробь.

Выглядит следующим образом:

S = ½ * а * h,

где:
S – площадь треугольника,
а – длина его стороны,
h – высота, опущенной на эту сторону.

Длина стороны и высота должны быть представлены в одинаковых единицах измерения. При этом площадь треугольника получится в соответствующих « » единицах.

Пример.
На одну из сторон разностороннего треугольника длиной 20 см, опущен перпендикуляр из противоположной вершины длиной 10 см.
Требуется площадь треугольника.
Решение.
S = ½ * 20 * 10 = 100 (см²).

Если известны длины двух любых сторон разностороннего треугольника и угол между ними, то воспользуйтесь формулой:

S = ½ * а * b * sinγ,

где: а, b – длины двух произвольных сторон, а γ – величина угла между ними.

На практике, например, при измерении площади земельных участков, использование вышеприведенных формул иногда бывает затруднительно, так как требует дополнительных построений и измерения углов.

Если вам известны длины всех трех сторон разностороннего треугольника, то воспользуйтесь формулой Герона:

S = √(p(p-a)(p-b)(p-c)),

a, b, c – длины сторон треугольника,
р – полупериметр: p = (a+b+c)/2.

Если кроме длин всех сторон известен радиус вписанной в треугольник окружности, то воспользуйтесь следующей компактной формулой:

где: r – радиус вписанной окружности (р – полупериметр).

Для вычисления площади разностороннего треугольника через радиус описанной окружности и длины его сторон, используйте формулу:

где: R – радиус описанной окружности.

Если известна длина одной из сторон треугольника и величины трех углов (в принципе, достаточно двух – величина третьего вычисляется из равенства суммы трех углов треугольника - 180º), то воспользуйтесь формулой:

S = (a² * sinβ * sinγ)/2sinα,

где α – величина противолежащего стороне а угла;
β, γ – величины остальных двух углов треугольника.

Правильным треугольником называют треугольник с тремя равными сторонами. Он обладает следующими свойствами: все стороны правильного треугольника равны между собой, а все углы равны 60 градусам. Правильный треугольник является равнобедренным.

Вам понадобится

• Знания по геометрии.

Инструкция

Пусть дана сторона правильного треугольника с длиной a=7. Зная сторону такого треугольника можно легко вычислить его площадь. Для этого используется следующая : S = (3^(1/2)*a^2)/4. Подставим в это формулу значение а=7 и получим следующее: S = (7*7*3^1/2)/4 = 49 * 1,7 / 4 = 20,82. Таким образом получили, что площадь равностороннего треугольника со стороной а=7 равна S=20,82.

Если дан радиус окружности, то будет выглядеть следующим образом:
S = 3*3^(1/2)*r^2, где r - радиус вписанной окружности. Пусть радиус вписанной окружности r=4. Подставим его в написанную ранее формулу и получим следующее выражение: S = 3*1,7*4*4 = 81,6. То есть при радиусе вписанной окружности равного 4 площадь равностороннего треугольника будет равна 81,6.

При известном радиусе описанной окружности формула площади треугольника выглядит так: S = 3*3^(1/2)*R^2/4, где R - радиус описанной окружности. Допустим, что R=5, подставим это значение в формулу: S = 3*1,7*25/4 = 31,9. Получается, что при радиусе описанной окружности равного 5 площадь треугольника равна 31,9.

Обратите внимание

Площадь треугольника всегда величина положительная, также как и длина стороны треугольника и радиусы вписанной и описанной окружностей.

Полезный совет

Радиус вписанной и описанной окружности в равностороннем треугольнике отличается в два раза, зная это, можно запомнить только одну формулу, например через радиус вписанной окружности, а вторую выводить, зная это утверждение.

Если известны длина одной из сторон треугольника и величины прилегающих к ней углов, его площадь можно вычислить несколькими способами. Каждая из формул вычисления предполагает использование тригонометрических функций, но это не должно пугать - для их расчета достаточно иметь доступ в интернет, не говоря уже о наличии в операционной системе встроенного калькулятора.

Инструкция

Первый вариант вычисления площади (S) по известной длине одной из сторон (A) и величинам прилегающих к ней углов (α и β) предполагает вычисление этих углов. Площадь в этом случае будет квадрату длины известной стороны, разделенному на удвоенную котангенсов известных углов: S = A*A/(2*(ctg(α)+ctg(β))). Например, если длина известной стороны равна 15 см, а величины прилегающих к ней углов равны 40° и 60°, то расчет площади будет выглядеть так: 15*15/(2*(ctg(40)+ctg(60))) = 225/(2*(-0.895082918+3.12460562)) = 225/4.4590454 = 50.4592305 квадратных сантиметров.

Второй вариант вычисления площади вместо котангенсов использует синусы известных углов. В этом варианте площадь равна квадрату длины известной стороны, умноженному на синусы каждого из углов и разделенному на удвоенный синус суммы этих углов: S = A*A*sin(α)*sin(β)/(2*sin(α + β)). Например, для того же треугольника с известной стороной в 15 см, и прилегающими к ней углами в 40° и 60°, расчет площади будет выглядеть так: (15*15*sin(40)*sin(60))/(2*sin(40+60)) = 225*0.74511316*(-0.304810621)/(2*(-0.506365641)) = -51.1016411/-1.01273128 = 50.4592305 квадратных сантиметров.

В третьем варианте вычисления площади треугольника задействованы тангенсы углов. Площадь будет равна квадрату длины известной стороны, умноженному на тангенсы каждого из углов и деленному на удвоенную сумму тангенсов этих углов: S = A*A*tg(α)*tg(β)/2(tg(α)+tg(β)). Например, для использованного в предыдущих шагах треугольника со стороной в 15 см и прилегающими углами в 40° и 60°, расчет площади будет выглядеть так: (15*15*tg(40)*tg(60))/(2*(tg(40)+tg(60)) = (225*(-1.11721493)*0.320040389)/(2*(-1.11721493+0.320040389)) = -80.4496277/-1.59434908 = 50.4592305 квадратных сантиметров.

Практические расчеты можно производить, например, с помощью калькулятора поисковой системы Google. Для этого достаточно подставить в формулы числовые значения и ввести их в поле поискового запроса.

Совет 4: Как найти площади треугольника и прямоугольника

Треугольник и прямоугольник - две простейшие плоские геометрические фигуры в Евклидовой геометрии. Внутри периметров, образованных сторонами этих многоугольников, заключен некоторый участок плоскости, площадь которого можно определить многими способами. Выбор способа в каждом конкретном случае будет зависеть от известных параметров фигур.

Треугольник - три точки, не лежащие на одной прямой, и три отрезка, которые их соединяют. Иначе, треугольник - это многоугольник, у которого имеется ровно три угла.

Указанные три точки называются вершинами треугольника, а отрезки - сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла.

Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны.

Равносторонним или правильным называется треугольник, у которого все три стороны равны. Все углы равностороннего треугольника также равны и равняются 60°.

Площадь произвольного треугольника вычисляется по формулам: или

Площадь прямоугольного треугольника вычисляется по формуле:

Площадь правильного или равностороннего треугольника вычисляется по формулам: или или

Где a ,b ,c - стороны треугольника, h - высота треугольника, y - угол между сторонами, R - радиус описанной окружности, r - радиус вписанной окружности.

Порой в жизни встречаются такие ситуации, когда приходится копаться в памяти в поисках давно забытых школьных знаний. Например, нужно определить площадь земельного участка треугольной формы или же пришел черед очередного ремонта в квартире или частном доме, и нужно посчитать, сколько уйдет материала для поверхности с треугольной формой. Было время, когда вы могли решить такую задачку за пару минут, а теперь отчаянно пытаетесь вспомнить, как же определить площадь треугольника?

Не стоит из-за этого переживать! Ведь это вполне нормально, когда мозг человека решает переложить давно неиспользуемые знания куда-нибудь в удаленный уголок, из которого порой их не так-то и легко извлечь. Чтобы вам не пришлось мучиться с поиском забытых школьных знаний для решения такой задачи, в этой статье собраны различные методы, которые позволяют легко найти искомую площадь треугольника.

Общеизвестно, что треугольником называют такой вид многоугольника, который ограничен минимально возможным количеством сторон. В принципе, любой многоугольник можно разделить на несколько треугольников, соединив его вершины отрезками, которые не пересекают его стороны. Поэтому, зная треугольника, можно посчитать площадь практически любой фигуры.

Среди всех возможных треугольников, которые встречаются в жизни, можно выделить следующие частные виды: и прямоугольный.

Проще всего площадь треугольника рассчитывается, когда один из его углов прямой, то есть в случае с прямоугольным треугольником. Несложно заметить, что он представляет собой половину прямоугольника. Поэтому его площадь равна половине произведения сторон, которые образуют между собой прямой угол.

Если нам известны высота треугольника, опущенная из одной из его вершин на противоположную сторону, и длина этой стороны, которую называют основанием, то площадь рассчитывается как половина произведения высоты на основание. Записывается это с помощью такой формулы:

S = 1/2*b*h, в которой

S - искомая площадь треугольника;

b, h - соответственно, высота и основание треугольника.

Так легко рассчитать площадь равнобедренного треугольника, поскольку высота будет делить противоположную сторону пополам, и ее легко можно будет измерить. Если определяется площадь то в качестве высоты удобно брать длину одной из сторон, образующих прямой угол.

Все это конечно хорошо, но как определить, является ли один из углов треугольника прямым или нет? Если размер нашей фигуры небольшой, то можно воспользоваться строительным углом, чертежным треугольником, открыткой или другим предметом с прямоугольной формой.

Но что делать, если у нас треугольный земельный участок? В этом случае поступают следующим образом: отсчитывают от вершины предполагаемого прямого угла по одной из сторон расстояние кратное 3 (30 см, 90 см, 3 м), а по другой стороне отмеряют в той же пропорции расстояние кратное 4 (40 см, 160 см, 4 м). Теперь нужно измерить расстояние между конечными точками этих двух отрезков. Если получилось значение кратное 5 (50 см, 250 см, 5 м), то можно утверждать, что угол прямой.

Если известно значение длины каждой из трех сторон нашей фигуры, то площадь треугольника можно определить, используя формулу Герона. Для того чтобы она имела более простой вид, применяют новую величину, которая называется полупериметром. Это сумма всех сторон нашего треугольника, разделенная пополам. После того как полупериметр посчитан, можно приступать к определению площади по формуле:

S = sqrt(p(p-a)(p-b)(p-c)), где

sqrt - квадратный корень;

p - значение полупериметра (p =(a+b+c)/2);

а,b,с - ребра (стороны) треугольника.

Но что делать, если треугольник имеет неправильную форму? Здесь возможны два способа. Первый из них состоит в том, чтобы попытаться разделить такую фигуру на два прямоугольных треугольника, сумму площадей которых посчитать отдельно, а затем сложить. Или же, если известен угол между двумя сторонами и размер этих сторон, то применить формулу:

S = 0.5 * ab * sinC, где

a,b - стороны треугольника;

с - величина угла между этими сторонами.

Последний случай на практике встречается редко, но тем не менее, в жизни все возможно, поэтому приведенная выше формула не будет лишней. Удачи в расчётах!

Понятие площади

Понятие площади любой геометрической фигуры, в частности треугольника, будем связывать с такой фигурой, как квадрат. За единицу площади любой геометрической фигуры будем принимать площадь квадрата, сторона которого равняется единице. Для полноты, вспомним два основных свойства для понятия площадей геометрических фигур.

Свойство 1: Если геометрические фигуры равны, то значения их площадей также равны.

Свойство 2: Любая фигура может быть разбита на несколько фигур. Причем площадь первоначальной фигуры равняется сумме значений площадей всех составляющих её фигур.

Рассмотрим пример.

Пример 1

Очевидно, что одна из сторон треугольника является диагональю прямоугольника , у которого одна сторона имеет длину $5$ (так как $5$ клеток), а вторая $6$ (так как $6$ клеток). Следовательно, площадь этого треугольника будет равняться половине такого прямоугольника. Площадь прямоугольника равняется

Тогда площадь треугольника равняется

Ответ: $15$.

Далее рассмотрим несколько методов для нахождения площадей треугольников, а именно с помощью высоты и основания, с помощью формулы Герона и площадь равностороннего треугольника.

Как найти площадь треугольника через высоту и основание

Теорема 1

Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.

Математически это выглядит следующим образом

$S=\frac{1}{2}αh$

где $a$ - длина стороны, $h$ - высота, проведенная к ней.

Доказательство.

Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.

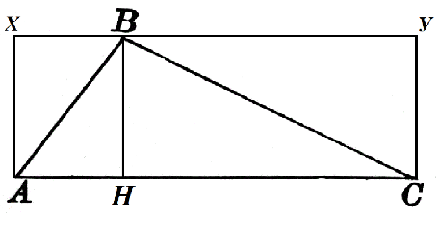
Площадь прямоугольника $AXBH$ равняется $h\cdot AH$, а прямоугольника $HBYC$ равняется $h\cdot HC$. Тогда

$S_ABH=\frac{1}{2}h\cdot AH$, $S_CBH=\frac{1}{2}h\cdot HC$

Следовательно, искомая площадь треугольника, по свойству 2, равняется

$S=S_ABH+S_CBH=\frac{1}{2}h\cdot AH+\frac{1}{2}h\cdot HC=\frac{1}{2}h\cdot (AH+HC)=\frac{1}{2}αh$

Теорема доказана.

Пример 2

Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице

Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим

$S=\frac{1}{2}\cdot 9\cdot 9=40,5$

Ответ: $40,5$.

Формула Герона

Теорема 2

Если нам даны три стороны треугольника $α$, $β$ и $γ$, то его площадь можно найти следующим образом

$S=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

здесь $ρ$ означает полупериметр этого треугольника.

Доказательство.

Рассмотрим следующий рисунок:

По теореме Пифагора из треугольника $ABH$ получим

Из треугольника $CBH$, по теореме Пифагора, имеем

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

Из этих двух соотношений получаем равенство

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac{γ^2-α^2+β^2}{2β}$

$h^2=γ^2-(\frac{γ^2-α^2+β^2}{2β})^2$

$h^2=\frac{(α^2-(γ-β)^2)((γ+β)^2-α^2)}{4β^2}$

$h^2=\frac{(α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α)}{4β^2}$

Так как $ρ=\frac{α+β+γ}{2}$, то $α+β+γ=2ρ$, значит

$h^2=\frac{2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α)}{4β^2}$

$h^2=\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2 }$

$h=\sqrt{\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2}}$

$h=\frac{2}{β}\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

По теореме 1, получим

$S=\frac{1}{2} βh=\frac{β}{2}\cdot \frac{2}{β} \sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$